Расчет простых трубопроводов. Простые и сложные трубопроводы
- gidroadmin
- 3155
Классификация трубопроводов
Движение жидкости в напорных трубопроводах происходит благодаря разности давлений (напоров) и начальном и конечном их сечениях. Эта разность может быть создана при помощи насоса, либо за счет уровня жидкости, либо под действием давления газа в резервуаре, из которого движется жидкость.
Все трубопроводы разделяются на простые и сложные. К простым относятся трубопроводы без разветвлений постоянного или переменного сечения, к сложным — трубопроводы с разветвлениями, составленные из последовательно и параллельно соединенных простых трубопроводов или ветвей. Особое место занимают трубопроводы с непрерывной раздачей жидкости, кольцевые, а также с насосной подачей (разомкнутые и замкнутые).
При гидравлическом расчете различают трубопроводы короткие и длинные. Короткими считаются трубопроводы сравнительно небольшой длины, в которых местные потери напора составляют не менее 5—10% потерь напора на трение по длине. При расчете их исходят из принципа наложения потерь, принимая Σhп=Σhдл + Σhмест. К коротким трубопроводам обычно относят масло- и топливопроводы двигателей внутреннего сгорания, системы жидкостного охлаждения, внутридомовую теплофикационную сеть, трубопроводы гидроприводов станков, транспортных средств и других машин.
Длинными считаются трубопроводы значительной протяженности, в которых потери напора на трение по длине являются основными, местные же потери составляют менее 5—10% потерь напора по длине. При расчете местные потери либо вовсе не учитывают, либо учитывают путем увеличения потерь напора на трение по длине на 5—10%. Таким образом, Σhп = (1,05 - 1,10)Σhдл. К длинным относят магистральные трубопроводы, неф- те- и газопроводы, водопроводные сети и др.
Расчет простых трубопроводов
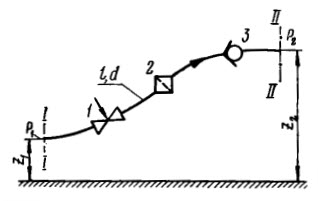 Для простого трубопровода
постоянного сечения (см рис.) длиной L, произвольно расположенного в
пространстве и содержащего ряд местных гидравлических сопротивлений, например вентиль 1, фильтр 2,
обратный кланан 3 и т.д., основным расчетным уравнением является уравнение Бернулли для начального
1 и конечного 2 сечений трубопровода, которое при α1 = α2 имеет вид:
Для простого трубопровода
постоянного сечения (см рис.) длиной L, произвольно расположенного в
пространстве и содержащего ряд местных гидравлических сопротивлений, например вентиль 1, фильтр 2,
обратный кланан 3 и т.д., основным расчетным уравнением является уравнение Бернулли для начального
1 и конечного 2 сечений трубопровода, которое при α1 = α2 имеет вид:
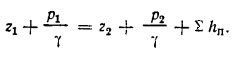
Суммарную потерю напора в общем случае удобно выразить формулой
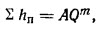
где А - сопротивление трубопровода.
При ламинарном режиме течения и замене местных гидравлических сопротивлений трубами эквивалентной длины m = 1 и
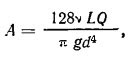
где расчетная длина трубопровода равна
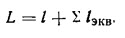
Строго говоря, при наличии в трубопроводе дросселя с квадратичным законом сопротивления замена его трубой не допустима. В этом случае потеря напора в дросселе оценивается по формуле Вейсбаха через коэффициент ξ
При турбулентном режиме течения и квадратичном законе сопротивления m = 2, и, как это следует из формул Дарси и Вейсбаха, если выразить скорости через расход,
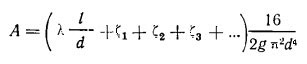
или
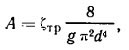
где ξ тр - коэффициент потерь в трубопроводе, равный выражению в круглых скобках в формуле выше.
Для трубопровода переменного сечения, состоящего из n участков начальное уравнение будет иметь вид:
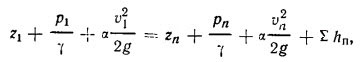
где индекс n означает конечное сечение, а сумма потерь hп складывается из потерь напора на всех n участках, т.е.
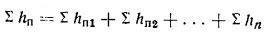
или
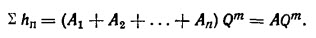
Вильнер Я.М. Справочное пособие по гидравлике, гидромашинам и гидроприводам.



 Рейтинг: 4.97
Рейтинг: 4.97
 Рейтинг: 4.8
Рейтинг: 4.8
 Рейтинг: 4.78
Рейтинг: 4.78
 Рейтинг: 4.76
Рейтинг: 4.76
 Рейтинг: 4.74
Рейтинг: 4.74