Уравнение Бернулли - основное уравнение гидравлики

В изучении основ гидравлики важное значение имеет знание и понимание уравнения Бурнулли. Кстати, Данниил Бернулии впервые опубликовал это уравнение в современном виде в 1738 г.

Для двух сечений потока 1—1 и 2—2 реальной жидкости (рисунок 1) при установившемся плавно изменяющемся движении уравнение Бернулли имеет вид:

z₁ + p₁/γ + α₁υ₁²/(2g) = z₂ + p₂/γ + α₂υ₂²/(2g) + Σh_п    (1)

где z — ордината, определяющая высоту положения центра выбранного сечения над произвольной горизонтальной плоскостью сравнения 0—0; p/γ — пьезометрическая высота; z + p/γ = H_п — гидростатический напор; αυ²/(2g) = h_v — скоростная высота, или скоростной напор; α — коэффициент Кориолиса, учитывающий неравномерность распределения скоростей в живом сечении потока.

Сумма трех членов:

z + p/γ + αυ²/(2g) = H

есть полный напор; Σh_п — потеря напора между выбранными сечениями потока. Вместо выражения (1) можно написать:

H₁ = H₂ + Σh_п

Все члены уравнения Бернулли в формуле (1) имеют линейную размерность и в энергетическом смысле представляют удельную энергию жидкости, т. е. энергию, отнесенную к единице веса жидкости.

Так, z и p/γ - удельная потенциальная энергия соответственно положения и давления;
z + p/γ - удельная потенциальная энергия жидкости;
αυ²/(2g) - удельная кинетическая энергия, выраженная через среднюю скорость потока в данном сечении. Сумма всех трех членов z + p/γ + αυ²/(2g) = H представляет полный запас удельной механической энергии жидкости в данном сечении потока;
Σh_п - удельная механическая энергия, затрачиваемая на преодоление сопротивления движению жидкости между сечениями потока и переходящая в тепловую энергию, которая состоит из следующих слагаемых:

Σh_п = Σh_дл + Σh_мест

где Σh_дл — потери энергии (напора) на трение по длине; Σh_мест — местные потери энергии (напора).

Если уравнение (1) умножить на γ, то получим:

γz₁ + p₁ + γα₁υ₁²/(2g) = γz₂ + p₂ + γα₂υ₂²/(2g) + γΣh_п    (2)

Члены уравнения (2) имеют размерность давления и представляют энергию, отнесенную к единице объема.

Если уравнение (1) умножить на g, то получим

gz₁ + p₁/ρ + α₁υ₁²/2 = gz₂ + p₂/ρ + α₂υ₂²/2 + gΣh_п     (3)

Члены уравнения (3) имеют размерность м²/с² и представляют энергию, отнесенную к единице массы.

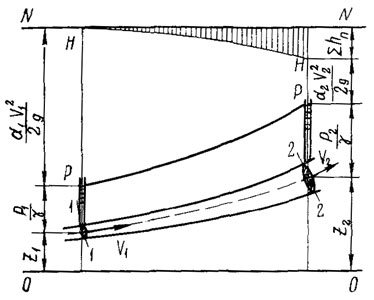
РИСУНОК 1

На рисунке 1 приведена диаграмма уравнения Бернулли для потока реальной жидкости. Здесь 0—0 — плоскость сравнения; N—N — плоскость начального напора; Н—Н — напорная линия, или линия полной удельной энергии. Падение ее на единицу длины представляет гидравлический уклон J; Р—Р — пьезометрическая линия, или линия удельной потенциальной энергии. Падение ее на единицу длины представляет пьезометрический уклон J_п.

Так как общий запас удельной энергии вдоль потока непрерывно уменьшается, линия Н—Н всегда нисходящая, а гидравлический уклон всегда положительный (J>0). Пьезометрическая линия может быть и нисходящей, и восходящей (последнее имеет место на расширяющихся участках, когда средняя скорость потока уменьшается), поэтому пьезометрический уклон может быть и положительным (J>0), и отрицательным(J<0).

На участках с равномерным движением жидкости, где имеют место только потери напора на трение по длине, линии Н — Н и Р — Р представляют взаимно параллельные прямые, поэтому J = J_п =h_дл/L. В этом случае потеря напора может быть определена по разности гидростатических напоров:

h_дл = (z₁ + p₁/γ) - (z₂ + p₂/γ)

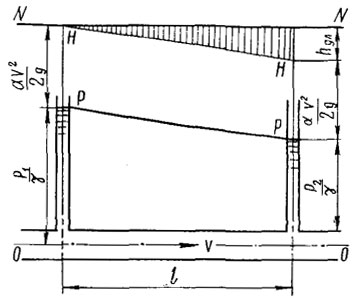
РИСУНОК 2

Для горизонтальных участков потоков (z₁=z₂) или в случае, если плоскость сравнения 0—0 проведена по оси потока (z₁=z₂=0) (рисунок 2), потеря напора на трение по длине может быть определена непосредственно по разности показаний пьезометров:

h_дл = (p₁ — p₂)/γ

На рисунке 3 показаны линия энергии Н — Н и пьезометрическая линия P — P для трубопровода переменного сечения, соединяющего два открытых резервуара.

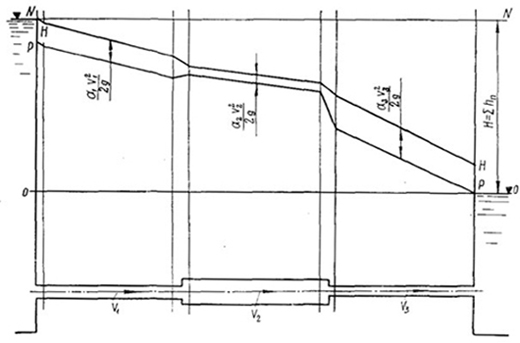
РИСУНОК 3

Уравнение Бернулли является ключевым в решении различных задач по гидравлике.

Подробное видео по теме "Уравнение Бернулли" приведено ниже.